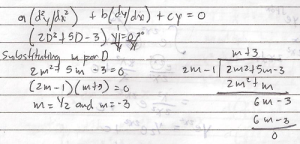Linear First and Second Order Differential Equation
Linear First Oder Differential Equation
The equation in the form dy/dx + Py = Q where P and Q are functions of x only is called Linear Differential Equations since y and its derivatives are of the first degree.
The solution for dy/dx + Py = Q is obtained by multiplying throughout by an Integrating factor ![]() to become
to become ![]()
Example: Solve the equation dy +4xy dx = 2xdx
Solution:
Rearranging: dy/dx + 4xy = 2x
then P = 4x and Q = 2x
Linear Second Order Differential Equation
Equation in the form a (d^2y/dx^2) + b(dy/dx) + cy = 0 where a, b, and c are constants, is called a linear second order differential equation with constant coefficient
Setting D = d/dx and D^2 = d^2/dx. The following procedures may be followed.
- write the equation in D – operator form (aD^2 + bD + C) y=0, substitute m for D and solve the auxiliary equation am^2 + bm + c=0 for m
A. If the roots are real and different (b^2 > 4ac) say ![]() .
.
B. If the roots are real and equal ![]() twice the general solution is
twice the general solution is ![]()
C. If the roots are imaginary (b^2 – 4ac) Say ![]()
Example: Solve the equation 2(d^2y/dx^2) + 5(dy/dx) – 3y = 0
Solution:
Writing D – operator form: (2D^2 + 5D – 3) y = 0
Substituting m for D gives the auxiliary equation 2m^2 + 5m – 3 = 0 which can be factored as (2m – 1) (m + 3) and the roots are m = ½ and m = -3
Since the roots are real and different the general solution is ![]()