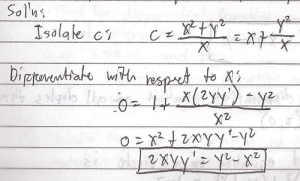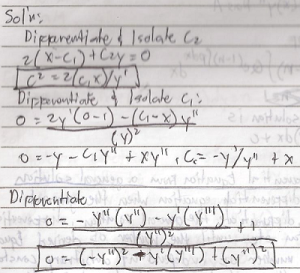To find the differential equation when the general solution is given, differentiate the general solution, differentiate the derived solution etc. until the number of derived equation is equal to the number of independent arbitrary constant finally eliminate the constants from the derived equations.
Finding the Differential Equation from a General Solution Examples
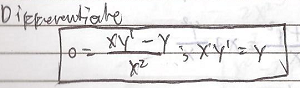
Example # 1:
Find the differential equation of X^2 + Y^2 = CX
Example # 2:
Find the Differential Equation of ( X – C1 )^2 + C2y = C3
Example # 3:
Find the differential Equation of all lines through the origin is
y = mx
m = y/x
Example # 4:
Find the differential equation of all circles through (0,0) and (2,0)
Solution:
The standard equation of a circle is (x-h)^2 + (y-k)^2 = 1-2