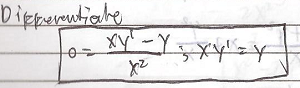
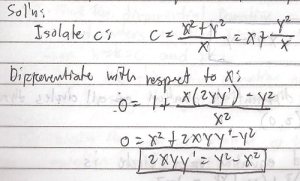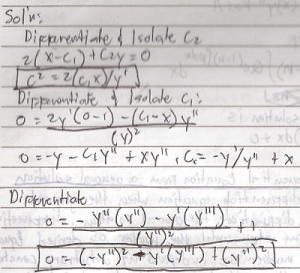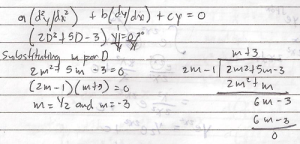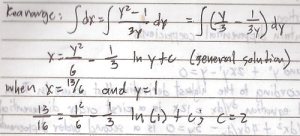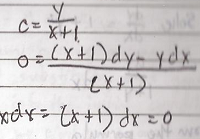differential equations Archives

December 1, 2014

Classification of Differential Equation and Examples

Classification of Differential Equation and Examples

1. Ordinary differential equation in which all derivatives are ordinary derivatives of one or more dependent variable with respect to a single independent variable.

2. A partial differential equation is a differential equation containing at least one partial derivative of some dependent variable.

3. The Order of a Differential Equation is the order of the neglect order derivative which appears in the equation.

4. A Differential Equation is linear in a set of one or more of its dependent variables if and only if each learn of the equation which contains a variable of the set or any of their duration is of the first degree in those variable and their derivative.

5. A Differential Equation which is not linear in some dependent variable is said to be nonlinear in that variables. A differential Equation which is not linear in the set of all its dependent variable is simply said to be nonlinear.

Example 1

The Equation is a linear differential equation of second order the presence of product xy and the term Cos X does not alter this fact that the equation is linear because by definition linearity is determined so Let y by the way the dependent variable y. and its derivatives enter into combination away themselves within each term of the equation.

Example 2

The Equation is a nonlinear equation becomes of the occurrence of the product of y and one of derivatives.

Example 3

The Equation is linear in the dependent variable V but nonlinear in the dependent variable a because Sin U is a nonlinear function of U. The equation is also nonlinear

Example 4

The Equation is linear in each dependent variable x and y. However because of the term xy is not linear in the set of dependent variable (x, y) or consequence the equation is also nonlinear.

Example 5

The equation 3x^2 dx + (Sin x) y = 0 is neither linear or nonlinear division by dx transform it into the equation 3x^2 + (Sin x) y = 0 which is linear in y but division by dy gives 3x^2 dx/dy + Sin x = 0

November 13, 2014November 13, 2014

Finding the Differential Equation from a General Solution

To find the differential equation when the general solution is given, differentiate the general solution, differentiate the derived solution etc. until the number of derived equation is equal to the number of independent arbitrary constant finally eliminate the constants from the derived equations.

Finding the Differential Equation from a General Solution Examples

Example # 1:

Find the differential equation of X^2 + Y^2 = CX

Example # 2:

Find the Differential Equation of ( X – C1 )^2 + C2y = C3

Example # 3:

Find the differential Equation of all lines through the origin is

y = mx

m = y/x

Example # 4:

Find the differential equation of all circles through (0,0) and (2,0)

Solution:

The standard equation of a circle is (x-h)^2 + (y-k)^2 = 1-2

November 12, 2014November 12, 2014

Linear First and Second Order Differential Equation

Linear First and Second Order Differential Equation

Linear First Oder Differential Equation

The equation in the form dy/dx + Py = Q where P and Q are functions of x only is called Linear Differential Equations since y and its derivatives are of the first degree.

The solution for dy/dx + Py = Q is obtained by multiplying throughout by an Integrating factor to become

Example: Solve the equation dy +4xy dx = 2xdx

Solution:

Rearranging: dy/dx + 4xy = 2x

then P = 4x and Q = 2x

Linear Second Order Differential Equation

Equation in the form a (d^2y/dx^2) + b(dy/dx) + cy = 0 where a, b, and c are constants, is called a linear second order differential equation with constant coefficient

Setting D = d/dx and D^2 = d^2/dx. The following procedures may be followed.

write the equation in D – operator form (aD^2 + bD + C) y=0, substitute m for D and solve the auxiliary equation am^2 + bm + c=0 for m

A. If the roots are real and different (b^2 > 4ac) say .

Then the general solution is

B. If the roots are real and equal twice the general solution is

C. If the roots are imaginary (b^2 – 4ac) Say

the general solution is

Example: Solve the equation 2(d^2y/dx^2) + 5(dy/dx) – 3y = 0

Solution:

Writing D – operator form: (2D^2 + 5D – 3) y = 0

Substituting m for D gives the auxiliary equation 2m^2 + 5m – 3 = 0 which can be factored as (2m – 1) (m + 3) and the roots are m = ½ and m = -3

Since the roots are real and different the general solution is

then the general solution is

November 11, 2014

How to Solve Differential Equation with Example

Differential Equation

– are equation that contain differential coefficients.

Example:

– classified according to the highest derivative that occurs in Them the differential equation dy/dx = 12x is a first order differential equation d^2y/dx^2 + 4dy/dx – 3y = 0 is a second order differential equation. A solution to a differential equation that contains one or more arbitrary constant of integration is called general solution. When additional information is Given so that these constants may be calculated the particular solution of differential equation is obtained.

Variable Separable

A differential equations can be of type dy/dx = f(x)solved by direct integration by writing it in the form dy = f(x) dx

Example:

Solve the differential equation dy/dx = 2x + Sin 3x

Solution: dy = (2x + Sin 3x) dx

y = x2 – 1/3 Cos 3x + c general solution

Differential equation of type dy/dx = f(y) can be solved by direct integrating by writing it in the form.

dx = dy/f(x)

Example:

Solve the equation (y^2 – 1) dy/dx = 3y Given that y = 1 when x = 13/6

Differential Equation of type

dy/dx = f(x) g(y) can be solve by Direct Integration by writing it in the form dy/g(y) = f(x)dx

Differential Equation of type dq/dt = KQ the general solution of an equation of the form dq/dt = KQ is Q = Ce^kt . where C is constant

Example:

solve the equation dy/dx = 3y

here we have Q = y dQ = dy then

t = x k = 3 y = Ce^3x

Example:

Obtain the differential equation of the family of straight lines with slope and y intercept equal

Solution:

The standard equation of the line in slope – intercept form is y = mx + b.

Since the slope and y intercept are equal m = b = c then y = cx + c

isolating constant and differentiate