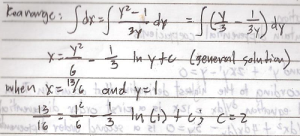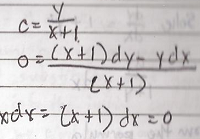How to Solve Differential Equation with Example
Differential Equation
– are equation that contain differential coefficients.
Example:
– classified according to the highest derivative that occurs in Them the differential equation dy/dx = 12x is a first order differential equation d^2y/dx^2 + 4dy/dx – 3y = 0 is a second order differential equation. A solution to a differential equation that contains one or more arbitrary constant of integration is called general solution. When additional information is Given so that these constants may be calculated the particular solution of differential equation is obtained.
Variable Separable
A differential equations can be of type dy/dx = f(x)solved by direct integration by writing it in the form dy = f(x) dx
Example:
Solve the differential equation dy/dx = 2x + Sin 3x
Solution: dy = (2x + Sin 3x) dx
y = x2 – 1/3 Cos 3x + c general solution
Differential equation of type dy/dx = f(y) can be solved by direct integrating by writing it in the form.
dx = dy/f(x)
Example:
Solve the equation (y^2 – 1) dy/dx = 3y Given that y = 1 when x = 13/6
Differential Equation of type
dy/dx = f(x) g(y) can be solve by Direct Integration by writing it in the form dy/g(y) = f(x)dx
Differential Equation of type dq/dt = KQ the general solution of an equation of the form dq/dt = KQ is Q = Ce^kt . where C is constant
Example:
solve the equation dy/dx = 3y
here we have Q = y dQ = dy then
t = x k = 3 y = Ce^3x
Example:
Obtain the differential equation of the family of straight lines with slope and y intercept equal
Solution:
The standard equation of the line in slope – intercept form is y = mx + b.
Since the slope and y intercept are equal m = b = c then y = cx + c
isolating constant and differentiate