Notebook Archives - Glen Nolasco

March 11, 2015July 9, 2023

Some Basic Concepts of Network Analysis

Basic Electrical Quantities

Electric Current (in a device) – designated by i(t), a function of time and is measured in amperes.

Electromotive Force (across a device) – designated by v(t), a function of time and is measured in volts.

Electric material can be broadly classified as: conductors and non-conductors (insulator).

The electric voltage across a perfect conductor must be zero and the electric current through a perfect insulator must be zero.

In network analysis we set these conditions mathematically by applying a short circuit (perfect conductor) and an open circuit (perfect insulator), respectively in the network.

3 types of diagrams to represent the network:

1. Pictorial schematic diagram – one that looks somewhat like the network represented.

2. Interconnection diagram – consists of a set of oriented line segments that indicate the pairs of points in the network at which measurements would be made to correspond with chosen network variables and that indicate the polarity of these measurements.

3. Schematic diagram – has the same geometry and orientation as a network interconnection diagram.

Instantaneous Meter – type of measuring instrument that we need to correlate with our analysis effort is one that, at least conceptually, has zero time lag in its motion and indicates both positive and negative values.

The international System of Units (SI) – commonly used in network analysis.

Resistance – the unit for resistance is ohm.

Kirchoff’s Law – principles postulated in 1847 by Gustav Kirchoff, a German physicist.

Kirchoff’s Current Law (KCL) – in any network, the oriented sum of instantaneous currents at each node is equal to zero.

Kirchoff’s Voltage Law (KVL) – in any electric network, the oriented sum of instanteneous voltage around every loop is equal to zero.

Kirchoff’s Current Law (Alternate Form) – the oriented sum of the instantaneous current at any supermode of a network is equal to zero.

March 1, 2015March 1, 2015

Objectives of Network Analysis

Objectives of Network Analysis

1. To analyze a network or system to see what is required of the device.
2. To established confidence in its chances for success to answer the always nagging question, “will the actual network perform as required?”.
3. To open up the idea for changing a component of an operating network to make it more reliable, cheaper to manufacture, or more efficient.

Electric Network – defined as a collection of lumped electric components that are selected and interconnected to produce a desired response.

Electric Network – connection points in the components.

We can characterize any two-terminal component symbolically with a box and two lines drawn from the box to terminate on dots.

Symbolic representations of a two-terminal component.

What is important is that two terminals are symbolized, and that there should be an unambiguous correspondence between the terminals and the corresponding connection points of the components so represented.

Physical networks are made up of physical objects and are therefore of major interest to engineers. The analysis of a physical network is based on a mathematical model of the network. This mathematical model must take into account the characteristics of the network components and their interconnection patter. If an analysis is to be successful, it must produce numbers characterizing the network response that correspond, within a given tolerance, to numbers obtained form the physical network analyzed with appropriate measuring devices.

December 14, 2014

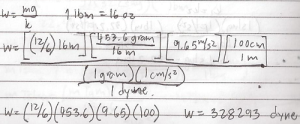
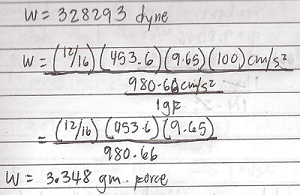Thermodynamics System and Surroundings

Thermodynamics System and Surroundings

System is the term given to the collection of matter under consideration enclosed within a Boundary.

Surroundings is the region outside the boundary or the space and matter external to a system.

Closed System is a system in which there is a flow of matter through the boundary.

Isolated System is a system in which wither mass nor energy cross the boundaries and it is not influence by the surrounding.

Non-Flow Process is a process that take place in a closed system.

Steady Flow Process is a process that takes place in an open system in which the quantity of matter within the system is constant.

Law of Conservation of Mass

Mass (M1) entering the system is equal to the sum of the stored mass ( _M) and the mass (M2) that leanes the system.

First Law of Thermodynamics

Energy cannot be created nor be destroyed it can only be transferred from one form to another.

Second Law of Thermodynamics

Heat cannot be transferred from cold body to an a heat body without an input of work. It similarly states that heat cannot be connected 100% into work. The Bottom line is that an engine must operate between a hot and cold reservoir.

Thrid Law

The total entropy of pure substances approaches zero at the absolute thermodynamics temp. Approaches Zero. Also indicated that energy has different levels of potential B.
Do work and that energy cannot naturally move from realm or lower potential to a realm of higher potential.

Zeroth Law

When any two Bodies are in Thermal Equilibrium with the third body. They are in Thermal Equilibrium with each other.

Heat

Form of energy associated with the kinetic random motion of large No. of molecules.

Sensible Heat

Heat needed to change the temp. of the Body without changing its phase.

Latent Heat

Heat needed by the body to change its phase without changing its temperature.

Latent Heat of Fusion of ICE = 144 13 tu/lb = 334 kj/ky

Latent Heat of Vaporization of Boiling H2O = 970 BN/bb = 2257 kj/ky

Entopy

Is the measure Boyle’s Law of randomness of the transferred to a substance at a constant pressure.

Internal Energy

Energy stored within the body sum of all kinetics energy of all its constituents particles plus the sum of all the potential energies of interaction among these articles if the temp is hold Constant the volume is inversely proportional to the absolute pressure.

Charles’s Law

If the absolute pressure is held constant the volume is directly proportional to the absolute temp.

General Gas Law

Even one of these laws states how one quantity varies with another if the third quantity remains unchanged but if the tree quantities chance simultaneously, it is necessary to combine these law’s in order

Temperature is an indication or degree of hotness and coldness and timeforce a measure of intensity of heat.

Six temp. Scales

Celcius
Farenheit
Kelvin
Rankine
Reamur
Ligem

Absolute Temperature

Is the temperature measure from absolute zero

December 1, 2014

Classification of Differential Equation and Examples

Classification of Differential Equation and Examples

1. Ordinary differential equation in which all derivatives are ordinary derivatives of one or more dependent variable with respect to a single independent variable.

2. A partial differential equation is a differential equation containing at least one partial derivative of some dependent variable.

3. The Order of a Differential Equation is the order of the neglect order derivative which appears in the equation.

4. A Differential Equation is linear in a set of one or more of its dependent variables if and only if each learn of the equation which contains a variable of the set or any of their duration is of the first degree in those variable and their derivative.

5. A Differential Equation which is not linear in some dependent variable is said to be nonlinear in that variables. A differential Equation which is not linear in the set of all its dependent variable is simply said to be nonlinear.

Example 1

The Equation is a linear differential equation of second order the presence of product xy and the term Cos X does not alter this fact that the equation is linear because by definition linearity is determined so Let y by the way the dependent variable y. and its derivatives enter into combination away themselves within each term of the equation.

Example 2

The Equation is a nonlinear equation becomes of the occurrence of the product of y and one of derivatives.

Example 3

The Equation is linear in the dependent variable V but nonlinear in the dependent variable a because Sin U is a nonlinear function of U. The equation is also nonlinear

Example 4

The Equation is linear in each dependent variable x and y. However because of the term xy is not linear in the set of dependent variable (x, y) or consequence the equation is also nonlinear.

Example 5

The equation 3x^2 dx + (Sin x) y = 0 is neither linear or nonlinear division by dx transform it into the equation 3x^2 + (Sin x) y = 0 which is linear in y but division by dy gives 3x^2 dx/dy + Sin x = 0

November 26, 2014

Engineering Mechanics Practice Problems

Engineering Mechanics Practice Problems

(REE – Apr. 2005)
1. Two boys B1 and B2 act at a point. The magnitude of B1 is 8 lbs and its direction is 60 degrees above the horizontal axis in the first quadrant. The magnitude of B2 is 5 lbs and its direction is 53 degrees below the horizontal axis in the fourth quadrant. What is the magnitude of the resultant force?

A. 7.0 lbs
B. 6.9 lbs
C. 7.6 lbs
D. 8.6 lbs

(REE – Apr. 2007)
2. Find the resultant value of two 10-lb forces applied by the two ladies at the same point when the angle between the forces is 30 deg. Use any convenient scale.

A. R = 20 lbs
B. R = 19.3 lbs
C. R = 15 lbs
D. R = 23 lbs

(REE – Sep. 2005)
3. Two 10-lb weights are suspended at opposite ends of a rope which passes over a light frictionless pulley. THe pulley is attached to a chain which goes to the ceiling. What is the tension in the rope?

A. 8 lbs
B. 10 lbs
C. 12 lbs
D. 20 lbs

(REE – Sep. 2001 / Sep. 2002 / Apr. 2005)
4. A safe weighing 600 lb is to be lowered at a constant speed down skids 8 ft long from a truck 4 ft high. If the coefficient of sliding friction between safe and skids is 0.30, whaat will you do with the safe? (REE – Sep. 2001)

A. nothing
B. hold back
C. push down
D. lift safe

How great a force parallel to the plane is needed? (REE – Sep. 2002 / Apr. 2005)

A. 140 lbs
B. 142 lbs
C. 146 lbs
D. 144 lbs

(REE – May 2009)
5. A roller whose diameter is 20 in. weighs 72 lbs. What horizontal force is necessary to pull the roller over a brick 2 In high, when the force is applied to the center?

A. 32 lbs
B. 30 lbs
C. 26 lbs
D. 24 lbs

(REE – May 2008)
6. An object weighing 425 N is held by a rope that passes over a horizontal drum. The coefficient of friction between the rope and the drum is 0.27. If the angle of contract is 160 deg. determine the force that will raise the object.

A. 871 N
B. 851 N
C. 881 N
D. 861 N

7. A car travels 30 km east and then 40 km north or a total distance of 70 km in a time of one hour.
A. What is the average speed?

A. 40kph
B. 50 kph
C. 60 kph
D. 70 kph

B. What is the average velocity?

A. 50 kph, N 53.13 deg E
B. 50 kph, E 53.13 deg N
C. 70 kph, N 53.13 deg E
D. 70 kph, E 53.13 deg N

(REE – Oct. 1996)
8. An automobile moving at a constant velocity of 15 m/sec passes a gasoline station. Two seconds later. another automobile leaves the gasoline station and accelerates at a constant rate of 2 m/sec sq. How soon will the second automobile overtake the first?

A. 15.3 sec
B. 16.8 sec.
C. 13.5 sec
D. 18.6 sec.

(REE – Apr. 2004)
9. Two piers A and B are located on a river, one mile apart. Two men must make round trips from pier A to pier B and return. One man is to row a boat at a velocity of 4 mi/hr relative to the water and the other man is to walk on the shore at a velocity of 4 mi/hr. The velocity of the river is 2 mi/hr in the direction from A to B. How long does it take each man to make the roundtrip?

A. 0.67 hr, 0.6 hr
B. 0.5 hr, 0.46 hr
C. 0.5 hr, 0.3 hr
D. 0.67 hr, 0.5 hr

(REE – Sep. 2007)
10. A stone is dropped from the top of a tall building and 1 sec later a second stone is thrown vertically down with a velocity of 60 ft/sec. How far below the top of the building will the second stone overtake the first?

A. 35.5 ft
B. 42.6 ft
C. 39.4 ft
D. 28.7 ft

(REE – Apr. 2007)
11. A student determine to test the law of gravity for himself walks off a skyscraper 900 ft high, stopwatch in hand and stars his free fall (zero initial velocty). Five seconds later, Superman arrives at the scene and dives off the roof to save the student. What must Superman’s initial velocity be in order that he catch the student just before the ground is reached? (Assume that Superman’s acceleration is that of any freely falling body).

A. 230 fps
B. 400 fps
C. 320 fps
D. 240 fps

(REE – Oct. 2000)
12. A student determined to test the law of gravity for he walks off a skyscraper stopwatch in hand, and starts his free fall (zero initial velocity). Five second later. Superman arrives at the scene and dives off the roof to save the student. What must be the height of the skyscraper so that even Superman can’t save him? (Assume that Superman’s acceleration is that of any freely falling body)

A. 200 ft
B. 300 ft
C. 400 ft
D. 500 ft

13. Water drips from a faucet at a uniform rate of 4 drops/second. Find the distance between two successive drops if the upper drop has been in motion for 3/8 second.

A. 0.613125 m
B. 1.22625 m
C. 1.916 m
D. 3.83 m

14. A stone is dropped from a cliff into the ocean. The sound of the impact of the stone on the ocean surface is heard 6.5 sec after it is dropped. The velocity of sound is 340 m/sec. How high is the cliff?

A. 22.10 m
B. 13.25 m
C. 175.61 m
D. 47.01 m

REE – Oct. 2000/ Apr. 2004
15. A ballon rising vertically with a velocity of 16 ft/sec, releases a sandbag at an instant when the balloon is 64 ft. above the ground. Compute the position of the sandbag 1/4 sec. after its release.

A. 5 ft
B. 3 ft
C. 1 ft
D. 2 ft

(REE – Apr. 2001/Sep. 2001)
16. A golf ball is driven horizontally from an elevated tee with a velocity of 80 ft/sec it strikes the fairway 2.5 sec. later. How far has it traveled horizontally?

A. 202 ft
B. 198 ft
C. 200 ft
D. 205 ft

(REE – Sep. 2005)
17. A golf ball is driven horizontally from an elevated tee with a velocty of 80 ft/sec it strikes the fairway 2.5 sec. later. How far has it traveled vertically?

A. 105 ft
B. 120 ft
C. 100 ft
D. 130 ft

(REE – Sep. 2008)
18. A Filipino football player kicks a football at an angle of 37 deg with the horizontal and with an initial velocity of 48 ft/sec. A second player standing at a distance of 100 ft from the first in the direction of the kicks starts running to meet the ball at the instant it is kicked. How fast must he run in order to catch the ball before it hits the ground?

A. 18.22 ft/sec
B. 17.22 ft/sec
C. 16.28 ft/sec
D. 19.46 ft/sec

19. A man who can throw a stone with a velocity of 25 m/sec wishes to hit a target T placed on his own level at a distance of 30 m. Neglecting the effects of air resistance, at what angle to the horizontal should he throw the stone?

A. 25 deg
B. 50 deg
C. 76 deg
D. 87 deg
20. A plane is flying horizontally 350 km per hour at an altitude of 420 m. At this instant, a bomb is released. How far horizontally from this point will the bomb hits the ground.

A. 785 m
B. 900 m
C. 625 m
D. 577 m

November 23, 2014November 23, 2014

Analysis of External Forces

Analysis of External Forces

Pxx – axial force. This components measured the pulling or pushing action perpendicular to the section a pull represents a Tensile force that tends to elongate the member. Where as a push is a compressive force that tends to shorten it. It is often denoted by P .

Pxy Pxz – sheurforces these are compounds of the total resistance to sliding the portion to one side of the exploratory section past the other. The resultant shear force is usually designated by V and its components by Vy and Vz to identify their directions.

Mxx – Torque this components measures the resistance to twisting the number and is commonly given the symbol T .

Mxy Mxz – Bending Moments these component, measures the resistance to bending the member about the y and z axes and are often denoted by My or Mz .

Example:
Consider two Bars of Equal length but of different materials suspended from a common support with a maximum axial loads 500N for BAR 1 and 500N for BAR 2, BAR 1 has a cross sectional are of 10mm² and for BAR 1 has an area of 1000 mm² which material is stronger.

November 23, 2014

Example of Superposition Theorem

Superposition Theorem Provides an alternative method for solving linear multisource circuits without the needs for simultaneous equations.

All of the supply sources but one are replaced by their own internal resistance or by a short circuit if the internal resistance is negligible.

The current distribution around the circuit is then solve by using ohms law.

This process is repeated the final current through each component is the Algebraic sum of currents produces when each source acted Alone.

Example of Superposition Theorem

Using the circuit values indicated by the CKT. Below, calculate the current through each resistor and the associated IR drops.

November 18, 2014

Vector Operations

Addition of vectors (2 Dimensional)

-there are two methods in adding series of vectors in 2 dimensional axes. They are the graphical & analytical methods.

Graphical Method:

This Method is used to determine the resultant of series of vectors graphically. This method is of two types, the parallelogram method and the polygon method.

Parallelogram Method

In this method, if we are going to determine the resultant of the three vectors, A, B & C, take the resulting vectors is added to the third vector which is vector C and the resulting vector is non the Final vector.

Example:

Given the vectors

Determine the resultant vector.

2. Polygon Method

In this method, we will connect the series of vectors graphically starting from A reference point up to the last vector then the resultant vector is the vector connecting from A reference point to the head of last vector.

Determine the resultant vector of the three vectors.

Analytical Method

This method is done through computation and this is of two types

1. Component Method

In this method the magnitude of the resultant vector is obtained by the formula

2. By Sine and Cosine law

Consider an Oblique triangle CDE with sides c, d and e.

Sine Law:

c/SinC = d/SinD = e/SinE

Cosine Law:

c^2 = d^2 + e^2 – 2de Cos C

d^2 = c^2 + e^2 – 2ce Cos D

e^2 = c^2 + d^2 – 2cd Cos E

November 16, 2014

Paralanguage

Paralanguage is a component of non-verbal communication that refers to those extra-linguistic elements such as voice quality, pitch, volume, and rate of speech that exist alongside the formal language structure.

Voice quality is the sound of voice.
Pitch is the highness or loudness of voice.
Volume is the loudness or softness of voice
Rate is how fast or slowly a person talks

Oculesics is the study of how eyes and eye movement can communicate.

Proxemics is the study of how people use space or distance for purposes of communication.

Haptics touching behavior is another form of Nonverbal symbol that may express a tremendous range of feelings.

Chronemics the study of time in communication is learned chronemics

Non verbal Communication – Benefits derived from Bodily action & Gestures.

1. They help breakdown stage fright

2. They are an outlet for nervous Energy

3. They are penetrate enthusiasm in the speaker

4. They Stimulate rapidity of thinking and fluency of utterance.

5. They reveal the personality of the Speaker.

6. They keep in the understanding the message.

Three types of gestures

1. Emphatic

2. Descriptive

3. Suggestive

Hand Gestures

1. Hand Supine – palm – upward.

– to show approval plan or request .

2. Hand adverse – palm outward, away from the body to show stronger feeling dissire and suppressed complete rejection.

3. Hand Index – First finger extended as of pouting to show or Point out an idea fasty a place or a person

4. Clended fist – to express great earnestaces or intensity of feeling.

November 16, 2014

Example of Thermodynamics Problems

Thermodynamics is a branch of physical science that treats various phenomena of heat, including the properties of matter, specially the laws of transformation of heat into other forms of energy and vice versa.

Matter – is anything that occupies space and has weight

Properties – characteristic of matter with is quantifiable

2 basic categories of properties of matter

Extensive – mass dependent
Intensive – mass independent

Extensive Properties

mass – Amount of matter in a substance
volume – space occupied by matter
weight – force exerted by gravity on a given mass

Mass weight relations

English Metric SI

W lbf kgf W

M slug hyl kgm

g Fb/s^2 m/s^2 m/s^2

a = 32.2ft/s^2 9.8 m/s^2 9.81 m/s^2

Second Law of Newton (Law of Motion)

– state that the acceleration of a particular body is directly proportional to the net force acting on it and inversely to its mass.

Example of Thermodynamics Problems with Solution

Problem # 1:

What is the weight of 66 kgm man at standard condition.

W = mg

m = kgm

g = 9.8

Problem # 2:

What is the weight of an object is 50lb. What is its at standard condition.

Problem # 3:

What is the mass in grams and the weight in dynes and gram force of 12 oz salt? Local acceleration is 9.65 m/s^2?

Problem # 4:

Five masses in a region where the acceleration due to gravity is 30.5 ft/s^2 are as follows: M1 is 500gm, M2 weighs 800gf, M3 weighs 15 poundals, M4 is 0.10 slug of mass. What is the total mass expressed in a pounds (b) slugs (c) grams.