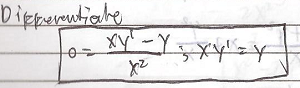
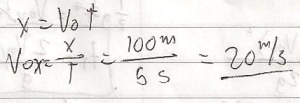
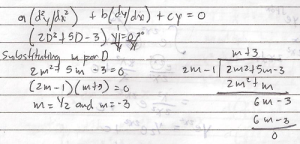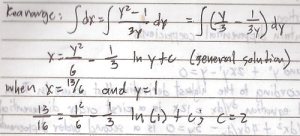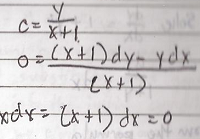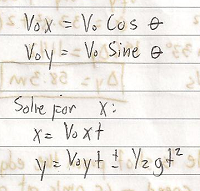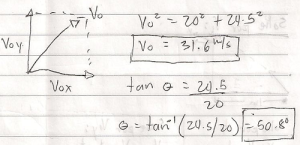Acquiring a second language is hard enough; learning a foreign tongue is even harder. This difficulty is particularly more pronounced in learning East Asian languages such as Japanese and Mandarin Chinese whose grammatical structure, orthography, and phonology seem too exotic for English users.
Thankfully, there is Bikol which, in my own classroom experience, provides the following learning aids:
a) prior knowledge upon which the students can build new learning;
b) cognitive landmark that may guide the students in navigating that complicated maze called foreign language acquisition and transitioning them from the familiar to the unknown; and
c) basis for analogy or comparison that may enhance comprehension.
FOREIGN VS. NATIVE SOUNDS & SYMBOLS
Teaching Japanese Phonetics
It is a well known fact that Japanese cannot produce the /l/ sound. This is not a racial predisposition. Perhaps, the Japanese are not able to develop the ability to perceive, hence, articulate the /l/ sound because such sound in nonexistent in their native language. By nature, such ability would find no usefulness.
And then there is this mistaken notion that the Japanese language is replete with the /r/ sound. Actually “r” is a mere symbol used to represent a sound that is midway between /r/ and /l/. This sound, although described as “midway between /r/ and /l/,” is actually closer to /d/.
The following texts that describe the Japanese /r/ and give suggestions on how it should be properly articulated were verbatimly lifted from authoritative sources and given to the students for them to understand.
“r—a sound peculiar to Japanese pronounced with the tip of the tongue moving midway in the mouth but not rolled. If the tongue is given slightly more tension, this sound easily becomes “d.” It is like neither “r” nor “l” in English but is sort of between the two, like the Spanish “r” in “pero.”
“/r/ is probably the most difficult sound for English-speaking students. This is neither /r/, /l/, nor /d/ in English, but may be most close to /d/. In Japanese it is necessary to distinguish /r/ and /d/.In both cases the tongue touches somewhere and comes off quickly and decisively. The difference between these /r/ and /d/ is that of the position of contact.
/r/ against the alveolar ridge with the very tip of the tongue
/d/ against the teeth with somewhere more front of the tongue”
“I put my foot in my mouth again today. When I introduced Miss Winters to my Japanese friends I meant to say Edo bungaku o kenkyuu shite imasu (She’s studying the literature of the Ed period). But my “d” sounded like an “r.” So what I actually said was “She’s studying pornographic literature” [Ero bungaku o kenkyuu shite imasu].”
“I then remembered what Sensee told me about the pronunciation of the “d” sound; I should have pressed the tip of the tongue against the upper teeth ridge.”
Teaching Japanese Orthography
Filipino students find the Japanese hiragana (cursive script) and katakana (angular script) too intimidating. They find such writing systems completely foreign. But using baybayin as springboard may somehow ease the intimidation and melt the resistance against learning them.
“Ra” is formed simply by adding a diacritic to “da.” Such process may also be used as springboard in teaching the transformation of basic kana characters into sonant and semisonant characters.
TEACHING JAPANESE & MANDARIN CHINESE GRAMMAR USING BIKOL THROUGH ANALOGY
Japanese Adjectives
Japanese adjectives are of two kinds: i-adjectives and na-adjectives.
I-adjectives, considered as true adjectives, are native to the Japanese language. They are so called because they end in character い(„i‟).
Example: oishii (delicious)
atsui (hot)
atatakai (warm)
When used as noun modifiers, i-adjectives behave like English adjectives, that is, they precede the nouns that they modify. For example:
oishii tabemono (delicious food)
atsui kōhii (hot coffee)
atatakai tenki (warm weather)
Na-adjectives are those that originated from Chinese and other foreign languages.
Example: shizuka (peaceful)
nigiyaka (lively)
shinsetsu (kind)
They are called na-adjectives because they need particle “na” when modifying nouns. For instance:
shizuka na machi (peaceful town)
nigiyaka na pātii (lively party)
shinsetsu na sensei (kind teacher)
Most students could not grasp the sense of the English translation because they could not account for the missing “na.” But translating the Japanese phrases into Bikol does the trick.
shizuka na machi (matoninong na banwa)
nigiyaka na pātii (maribok na party)
shinsetsu na sensei (maboot na maestra)
By employing Japanese-Bikol analogy, the Bikol translation enhances comprehension.
Mandarin Chinese Basic Sentence Pattern
The first sentence learned by a student of Mandarin Chinese is usually “Nǐ (you) hăo (fine).” It‟s literal translation is “you are fine,” but its equivalent expression in English is “Hi.”
“Nǐ hăo” may be expanded to “Nǐ hăo ma?” whose literal translation is “you are fine?” but is equivalent in English to “How are you?”
The formulaic response is “Wŏ (I) hăo” (I am fine) or “Wŏ hĕn (very) hăo” (I am very fine).
“Wŏ hăo” is the basic—being the simplest—sentence pattern in Mandarin Chinese. Ironically, it is its simplicity that makes it hard to comprehend. English users are told that a sentence may not be complete without a verb. But “Wŏ hăo” is a complete, albeit verbless sentence.
In Mandarin Chinese, when the complement is an adjective, a linking verb is not necessary, as in:
Wŏ hăo. (I am fine.)
Hànyŭ (Mandarin Chinese) nán (difficult). Mandarin Chinese is difficult.
But the complement is a noun, the linking verb “shì” is needed, as in:
Wŏ shì (am) Fēilǜbīnrén (Filipino). (I am [a] Filipino.)
Tā (she) shì lăoshī (teacher). (She is a teacher.)