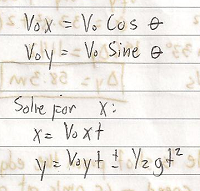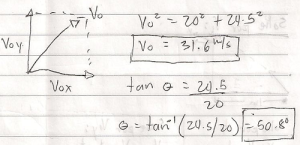Projectile Motion is a form of motion where a particle (called a projectile) is thrown obliquely near the earth’s surface, and it moves along a curved path under the action of gravity. The path followed by a projectile motion is called its trajectory. Projectile motion only occurs when there is one force applied at the beginning of the trajectory after which these is no interference apart from gravity.
These are the formulas to solve Projectile Problems.
Example of Projectile Motion Problems with Solution:
1. A stone is projected from the ground with a velocity of 15 m/s at an angle of 30 degree with the horizontal ground. How high in meter will it rise? Use g = 9.817 m/s/s.
Figure:
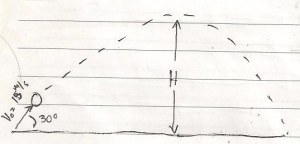
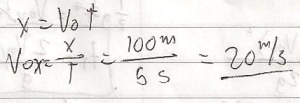
2. Former Bob and his horse Flash jump a 100m wide canyon. The flight through the air takes 5s. Find the initial velocity (That is, find the magnitude and the angle of the initial velocity)
1st You need to solve the vertical using the formula V = Vo + gt. Substitute the gravity and the time.
2nd Solve the horizontal, use the formula x = Vox times the time.
Use Pythagorean Theorem formula to solve initial Velocity and the Angle.
Answer: 31.3 m/s for the Initial Velocity , and 50.8 degree for the Angle.
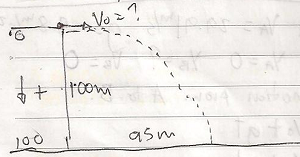
3. A rock is thrown horizontally off a 100m cliff. It lands 95m away. At what speed was it thrown?
4. A ball is thrown from a tower 30m high above the ground with a velocity of 300 m/s directed at 20 degree from the horizontal. How long will the ball hit the ground?
5. A Projectile is shot from edge of a cliff 125m above ground level with an Initial speed of 65 m/s at an angle of 37 degree above the horizontal. Determine the magnitude and the direction of the velocity at the maximum height.
Answer: The Projectile’s velocity at its max height is completely horizontal, and this is the same as the initial horizontal velocity.
Vf = Vix
= 65Cos 37
= 51.9 m/s (forward/horizontal)