Vector Operations
Addition of vectors (2 Dimensional)
-there are two methods in adding series of vectors in 2 dimensional axes. They are the graphical & analytical methods.
Graphical Method:
This Method is used to determine the resultant of series of vectors graphically. This method is of two types, the parallelogram method and the polygon method.
- Parallelogram Method
In this method, if we are going to determine the resultant of the three vectors, A, B & C, take the resulting vectors is added to the third vector which is vector C and the resulting vector is non the Final vector.
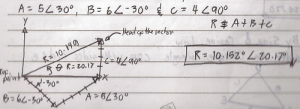
Example:
Determine the resultant vector.
2. Polygon Method
In this method, we will connect the series of vectors graphically starting from A reference point up to the last vector then the resultant vector is the vector connecting from A reference point to the head of last vector.
Determine the resultant vector of the three vectors.
Analytical Method
This method is done through computation and this is of two types
1. Component Method
In this method the magnitude of the resultant vector is obtained by the formula
2. By Sine and Cosine law
Consider an Oblique triangle CDE with sides c, d and e.
Sine Law:
c/SinC = d/SinD = e/SinE
Cosine Law:
c^2 = d^2 + e^2 – 2de Cos C
d^2 = c^2 + e^2 – 2ce Cos D
e^2 = c^2 + d^2 – 2cd Cos E